Introduction to Engineering Materials

In the industry most of the time, it is important for the NDT inspector to be able to locate the source of the problem when it exists, or even when a fault is not located, know that the possibility of one exists. An understanding of the materials, the processes, and the possible interactions between them is, therefore, a must for an NDT Inspector. Hence in this article, we will learn about Engineering material and a brief about different types of Engineering Materials.

What is Material?

Material is a substance or mixture of substances that constitute an object.

Materials can be pure or impure, living, or non-living matter. They can be classified based on their physical and chemical properties, or on their geological origin or biological function. Materials science is the study of materials and their applications.

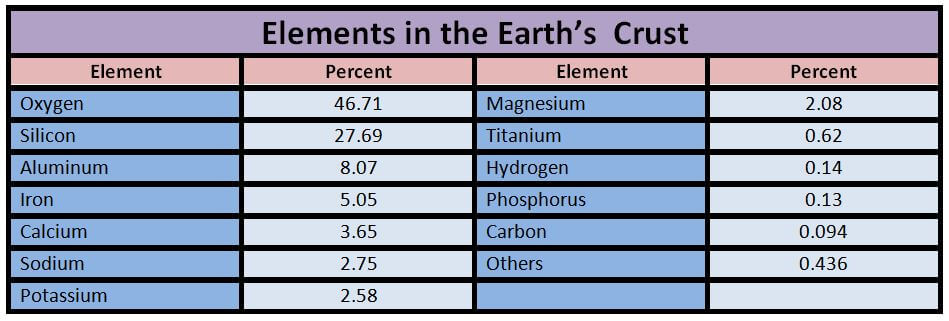
What are the engineering materials?

Engineering materials refers to the group of materials that are used in the construction of man-made structures and components. The primary function of an engineering material is to withstand applied loading without breaking and without exhibiting excessive deflection.

Metals can be classified as

• Ferrous
• Non-Ferrous

Ferrous Metals

“ferrous” means generally “containing iron“. The word is derived from the Latin word Ferrum (“iron”). Ferrous metals include steel and pig iron (with a carbon content of a few percent) and alloys of iron with others.

Ferrous materials containing iron, and steel is the most important material of this family. Because of availability, low cost, high strength, ease of fabrication into many shapes, and a wide range of properties, steel accounts for 80% of all metallic materials. It is widely used in manufacturing, building and construction industries.

Ferrous metals have high carbon content which generally makes them vulnerable to rust when exposed to moisture. There are two exceptions to this rule: wrought iron resists rust due to its purity and stainless steel is protected from rust by the presence of chromium.Most ferrous metals are magnetic which makes them very useful for motor and electrical applications.

Ferrous metals are used in shipping containers, industrial piping, automobiles, railroad tracks, and many commercial and domestic tools.

Nonferrous Metals

Non-ferrous metal and alloys, does not contain iron (ferrite) in appreciable amounts. Non-ferrous metals were the first metals used by humans for metallurgy. Copper was the first metal to be forged.

Important non-ferrous metals include

• Aluminum, copper, lead, nickel, tin, titanium, and zinc,
• Precious metals such as gold, silver and platinum and exotic or
• Exotic or rare metals such as cobalt, mercury, tungsten, beryllium, bismuth, cerium, cadmium, niobium, indium, gallium, germanium, lithium, selenium, tantalum, tellurium, vanadium, and zirconium.

Non-Metals

In chemistry, a nonmetal is a chemical element that mostly lacks the characteristics of a metal. Physically, a nonmetal tends to have a relatively low melting point, boiling point, and density. A nonmetal is typically brittle when solid and usually has poor thermal conductivity and electrical conductivity

Some Types of Non-metals

• Ceramics
• Glasses
• Plastic
• Elastomers

Ceramics

A ceramic is a solid material comprising an inorganic compound of metal or metalloid and non-metal with ionic or covalent bonds.

Ceramic engineering is the science and technology of creating objects from inorganic, non-metallic materials. This is done either by the action of heat or at lower temperatures using precipitation reactions from high-purity chemical solutions.

Properties  of Ceramics:

Compared to metals and plastics, ceramics are hard, non-combustible, and inert. Ceramic materials are usually ionic or covalent bonded materials and can be crystalline or amorphous,have high melting points,Good hardness, strength and durability, have Low electrical and thermal conductivity.

 Glasses

Glass is a non-crystalline, amorphous solid. Glass is most often formed by rapid cooling (quenching) of the molten form; some glasses such as volcanic glass are naturally occurring.

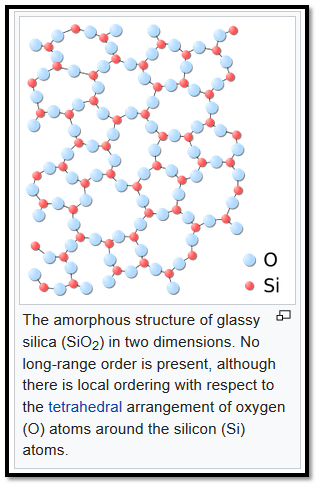
Usually, glass is brittle and will fracture, unless it is laminated or tempered to enhance durability, typically inert, resistant to chemical attack, and can mostly withstand the action of water, have low ductility; they are very brittle, have low thermal conductivity compared to metals, can be good electrical insulators.

key  Optical properties of glasses refractive index, dispersion, and transmission, making them superior to clear plastics for lenses, sight glasses and windows.

Types of glass

• Silicate glass.
• Soda-lime
• glass Borosilicate glass
• Lead glass
• Aluminosilicate glass
• Glass-ceramics
• Fibreglass
• Silica-free glass

Plastics/Polymers

Chemically plastics are called polymers.

IUPAC (International Union of Pure and Applied Chemistry) definition of plastic.

A polymer is a substance composed of macromolecules. A macromolecule is a molecule of high relative molecular mass, the structure of which essentially comprises the multiple repetitions of units derived, actually or conceptually, from molecules of low relative molecular mass.

The smallest unit structure or molecule that identifies the chemical involved is called a monomer. A polymer is a large molecule, or macromolecule, composed of many repeated monomers.

Polymerization is a process of reacting monomer molecules together in a chemical reaction to form polymer chains or three-dimensional networks.

Types of plastics

Elastomers

Rubber-like solids with elastic properties are called elastomers. An elastomer is a polymer with viscoelasticity (i.e., both viscosity and elasticity) and has very weak intermolecular forces.

IUPAC defines the term “elastomer” by “Polymer that displays rubber-like elasticity.”

Polymer chains are held together in these materials by relatively weak intermolecular bonds, which permit the polymers to stretch in response to macroscopic stresses. Elastomers are usually thermosets (requiring vulcanization) but may also be thermoplastic.

Vulcanization Is curing of elastomers. It works by forming cross-links between sections of the polymer chain which results in increased rigidity and durability, as well as other changes in the mechanical and electrical properties of the materials.

Conclusion

There are numerous numbers of engineering materials in the industry. we have to tried to cover the commonly used used basic types of engineering materials.

The purpose of NDT is to locate various faults in materials and products that have been processed to at least some degree. The flaws, defects or imperfection that may be located by inspection may be a result of the original material, caused by the processing used, created by some human error, or be a result of some combination of these.

NDT personnel need familiarity with many material characteristics in order to evaluate their suitability for service, through nondestructive testing. Determining the source or cause of defects is frequently necessary in order to eliminate these defects from production parts. Often the causes of defects lie in early farms or stages of material production or processing and in some cases these prior processes control the response of materials to later processes, during which defects or failures are induced.

References

• TWI global,
• Wikipedia.org
• Sciencedirect.com
• Materials and Processes for NDT Technology-ASNT
• https://www.glassallianceeurope.eu/
• Feature Photo by Robby McCullough on Unsplash